目錄
前言
由於碩士課程裡接觸到關於 Cryptography (密碼學) 的課題,突然對 Encryption (加密) 和 Decryption (解密) 的東西產生了興趣,所以寫下這篇文章,以防剛學完的東西轉眼又忘掉了。所謂 Encryption 就是把原有的文字訊息,轉換成一些沒意義的 Cipher (暗號)。而收到暗號的人把訊息還原,就是 Decryption。
Caesar cipher 凱撒密碼
早於古羅馬時代,已經出現加密技術。相傳凱撒大帝在行軍時,下達君令會把訊息加密。被加密的訊息到達將領手中就會進行解密。而加密的方法就是以特定方式把原有字母用其他字母取代,由於將領知道取代的方法,很容易就可把訊息解密,以下是一個例子:
| 原文 | a | b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | w | x | y | z |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 加密 | D | E | F | G | H | I | J | K | L | M | N | O | P | Q | R | S | T | U | V | W | X | Y | Z | A | B | C |
於是,如果原有訊息是:try to decrypt this message
加密後就會變成:wub wr ghfubsw wklv phvvdjh
所以如果你知道原文和加密訊息的替換方法,很容易就可以解密。以上的例子是把原文字母向右移動三格作為加密,又稱作 Key = 3。Key 就是發訊者與收訊者共同協議的加密解密鑰匙。
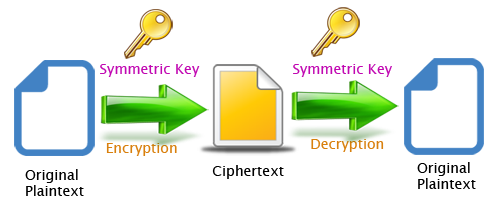
又由於加密和解密都是用同一條 Key,這條 Key 就稱為 Symmetric Key,而這種 Encryption 亦稱為 Symmetric Encryption。
不過 Caesar Cipher 這個加密方法有個嚴重的缺陷,就是只有 25 個替換的選擇,亦即是只有 25 條 Key,如果加密訊息被敵人截獲,只需把 25 條 Key 逐一嘗試,很快便能破解加密訊息。
既然問題在於 Key 的數量不足,怎樣可解決這個問題呢?後來就有人想到,不要順序把字母編碼,取而代之的是隨機地把字母換成其他字母,例如:
| 原文 | a | b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | w | x | y | z |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 加密 | I | G | W | V | A | H | U | J | T | S | B | R | K | Q | C | P | L | Y | O | E | N | X | M | D | Z | F |
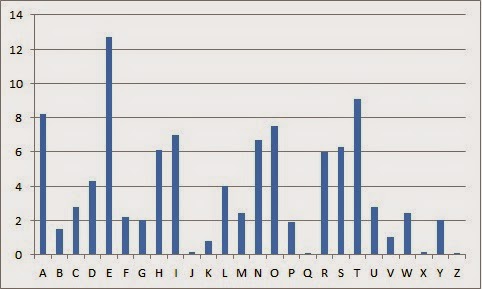
像這樣隨機加密,Key 的數目就會等於 26! = 400,000,000,000,000,000,000,000,000 條 Key 可以使用,這就解決了敵方逐一嘗試的可能性。可是,針對這種加密方法的破解技術出現了!就是 Frequency Analysis (頻率分析)。
大家有沒有想過,在一篇文章中,不同字母出現的機率並非完全相同的,例如:a,e,i 等字母出現的較多,q, x, z 則較少。再加上,我們知道單個英文字母出現的話肯定是 I 或者 a,兩個英文字母多數是:of, to, in, it, is, be 等等,如果字母重覆出現,就很可能是 ss, ee, tt, ff 等等。利用這些特點,只要密文夠長的話,就能有機會分析到密文所對應的字母。
你有張良計,我有過牆梯。要防止 Frequency Analysis 的攻擊,加密者可以使用以下幾個方法:
- 字與字之間不使用分隔
- 故意串錯字
- 加入一些沒意義的字母
- 把特定字換成其他字,例如:把 is 換成 ztp,把 the 換成 kagg 等
可是這些方法都會增加解密的難度,而且,只要時間充足的話,攻擊者一樣可以把密文分析出來。
Vigenère Cipher 維吉尼亞密碼
到了十六世紀,加密法有了新的突破!法國人維吉尼亞用了一個以其名命的加密方法。首先加密者準備一份維吉尼亞表格,這表格其實就是凱撒密碼的變體,只不過是把所有 Key 列出來。
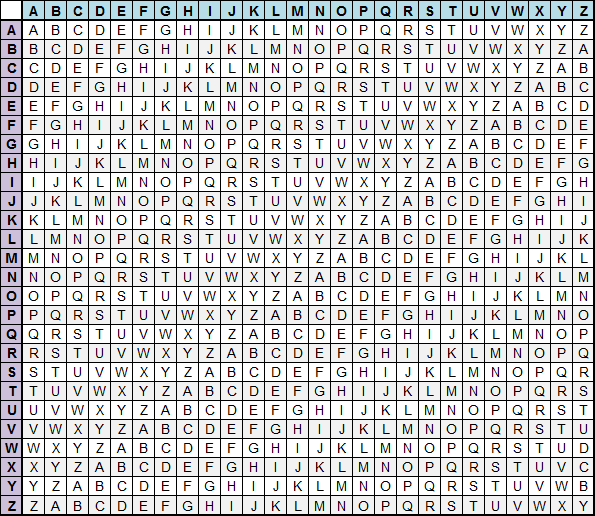
發訊者與收訊者先協商好一條 Key,而 Key 是任何一組英文字,在以下的例子,我們使用 WHITE 來做 Key。原文為 divert troops to eastridge,加密的方法是使用對應 KEY 的一行維吉尼亞表格來置換字母。
| Key | W | H | I | T | E | W | H | I | T | E | W | H | I | T | E | W | H | I | T | E | W | H | I |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 原文 | d | i | v | e | r | t | t | r | o | o | p | s | t | o | e | a | s | t | r | i | d | g | e |
| 加密 | Z | P | D | X | V | P | A | Z | H | S | L | Z | B | H | I | W | Z | B | K | M | Z | N | M |
維吉尼亞密碼最妙的地方是就算同一個原文字母會被加密成不同的加密字母,有效地抵抗 Frequency Analysis 的攻擊。
可惜,道高一呎,魔高一丈!過了不久,就有人想到破解方法。試看看以下一組維吉尼亞密碼:
| Key | K | I | N | G | K | I | N | G | K | I | N | G | K | I | N | G | K | I | N | G | K | I | N | G |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 原文 | t | h | e | s | u | n | a | n | d | t | h | e | m | a | n | i | n | t | h | e | m | o | o | n |
| 加密 | D | P | R | Y | E | V | N | T | N | B | U | K | W | I | A | O | X | B | U | K | W | W | B | T |
留意 BUK 曾經兩度出現,這種巧合讓攻擊者想到 Key 可能在這裡循環了兩次。攻擊者這時會嘗試代入三個英文字母的字詞來嘗試找出 key。這種重覆性就是攻擊者破解的關鍵,如果原文夠長的話,攻擊者就可以利用這點拆解出原文。
到此刻為止,在密碼學的戰爭中,攻擊者似乎大獲全勝……
奇謎密碼機 (Enigma)
就這樣過了一段很漫長的歲月,故事來到 20 世紀初,發生了一件重大事件,讓密碼學的渴求更加激烈,就是無線電的發明!由於無線電透過大氣電波傳送,人人都有機會接收得到,因此秘密訊息如果想透過無線電傳播必需加密。無線電用於軍事上,然而人們開始意識到透過人手加密解密訊息,速度慢之餘,也限制了加密和解密演算的複雜程度。為了發展出更難破解的加密,密碼學進入了機械化的時代。
到了第一次世界大戰,德軍引進了奇迷密碼機。此款密碼機內置了大量齒輪組件,使用者輸入訊息時就會同時產生加密訊息,只要收發雙方知道 Key 的設定,就能彼此交換密碼訊息。這使加密者和破解者的戰爭進入白熱化的階段。

One-time Pad Encryption 一次性密碼本加密
終於,加密的歷史進入了電腦時代。由於數位處理只有 1 和 0,因此,電腦的加密是建構在 1 和 0 之間的轉換。比較常用的為 XOR (Exclusive or) 來作轉基楚。例如:明文訊息是 HELLO,密匙是 APPLE,把明文和密匙都轉換成 ASCII 再用 XOR 加密起來。
| Key | A 01000001 |
P 01010000 |
P 01010000 |
L 01001100 |
E 01000101 |
|---|---|---|---|---|---|
| 原文 | H 01001000 |
E 01000101 |
L 01001100 |
L 01001100 |
O 01001111 |
| 加密 | 00001001 | 00010101 | 00011100 | 00000000 | 00001010 |
如果想解密,只要將密文與 KEY 做一次 XOR 就能得到原文了。One-time Pad Encryption 做法簡單,而且很難攻破,唯一缺點是 Key 的長度必需和原文一樣長。
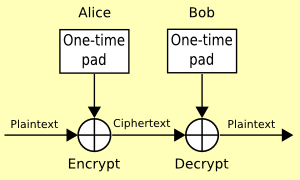
Stream Ciphers 資料流加密
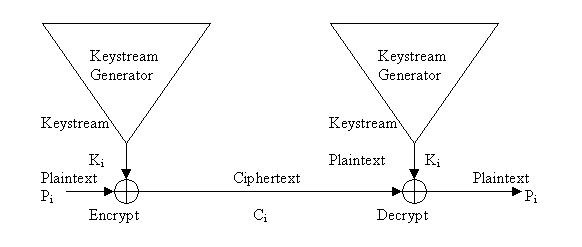
與 One-time Pad 相近的是 Stream Ciphers,當中所不同的是加密所用的 Key 不需與明文一樣長,Stream Ciphers 會把 Key 通過 Generator 延伸成無限長的 Keystream ,用來加密訊息。由於 Stream Ciphers 是把明文訊息逐個 Bit 轉換成 密文,特別適合串流訊息使用,例如:視像訊息,Voice 等等。較有名的 Stream Ciphers 是 RC4。
Block Ciphers 資料區段加密
ECB (Electronic Code Book)
另一種加密方式是 Block Ciphers。透過 Block Ciphers,明文訊息被斬開成一個個 Block,每一個 Block 被獨立地進行加密,最後把所有已加密的 Block 再組合起來,就是成為了密文,這個方法也稱之為 ECB (Electronic Code Book)。不過今次做 Encrypt 的演算法就不是用 XOR 這麽簡單。而是經過非常繁複的演算法 (algorithm) 產生出密文,例如:AES 和 DES 等,讓攻擊者無法反向猜到明文。
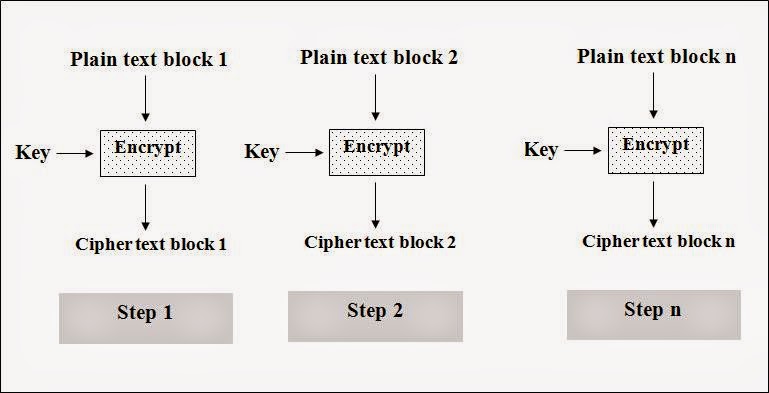
P = Plain Text, C= Cipher, K=Key
| Encryption: | Decryption: |
| C0 = Enc(K, P0) | P0 = Dec(K,C0) |
| C1 = Enc(K, P1) | P1 = Dec(K,C1) |
| . | . |
| . | . |
| . | . |
| Cn = Enc(K,Pn) | Pn = Dec(K,Cn) |
然而,ECB產生了一個問題,就是如果某些 Blocks 的內容一樣,所產生出來的密文必然相同,這就存在了保安問題,攻擊者有機會拆解出密文背後的秘密,最經典的例子是加密點陣圖 (Bitmap) 的問題。
假設我們用 ECB 把下方左圖加密,由於點陣圖檔案裡相同顏色的 Block 資料是一樣的,而相同顏色會產生出相同的密文訊息,因此圖片經加密後仍然隱約看到圖片的內容。
 |
 |
CBC (Cipher Block Chaining)
我們可以把 Block Ciphers 改良,解決這個問題,例如使用 CBC (Cipher Block Chaining)。CBC Mode 的重點是每一個 Block 的明文都會先和上一個 Block 的密文做一次 XOR,然後才進行 Encryption,因此就算明文是相同的,都會產生出不同的加密結果,如此一來,就解決了 ECB 所遇到的問題了。(Initial Vector 是一個任意起始值)
 |
 |
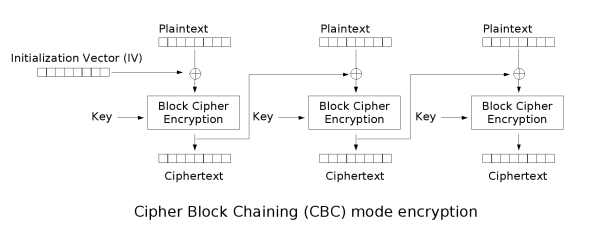
| Encryption: | Decryption: |
| C0 = Enc(K, P0⊕IV) | P0 = Dec(K,C0)⊕IV |
| C1 = Enc(K, P1⊕C0) | P1 = Dec(K,C1)⊕C0 |
| . | . |
| . | . |
| . | . |
| Cn = Enc(K,Pn⊕Pn-1) | Pn = Dec(K,Cn)⊕Cn-1 |
不過,由於在 CBC 中每一個加密訊息都需倚賴前一個加密訊息運算出來,因此,如果一個加密訊息 Block 有損毁,就會影響連續兩個加密訊息出現問題而無法解密。
CTR (Counter Mode)
另一種 Block Cipher 稱為 CTR (Counter Mode),加密流程如下圖:
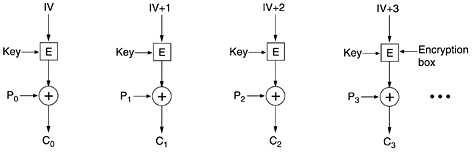
| Encryption: | Decryption: |
| C0 = P0⊕Enc(K, IV) | P0 = C0⊕Enc(K, IV) |
| C1 = P1⊕Enc(K, IV + 1) | P1 = C1⊕Enc(K, IV + 1) |
| . | . |
| . | . |
| . | . |
| Cn = Pn⊕Enc(K, IV + n) | Pn = Cn⊕Enc(K, IV + n) |
CTR 最妙的地方是在 Decryption 時不需要使用 Decryption Function,而是使用 Encryption Function 來進行解密。這在速度上有優勢,特別適合需要不斷讀寫的資料。但 CTR 最大的問題是一旦 IV 出了問題,或中途 IV 因為某些原因出錯了,所有之後的訊息就再也不能解密出來了!
CFB (Cipher Feedback Mode)
最後要介紹的是 CFB mode,與 CTR 相同的是,只需使用 Encryption Function 即可進行解密,不過比 CTR 的好的是 IV 的失誤只會導致第一個 Block 出問題。不過如果任何一個 Cn 出錯,仍然會導致連續兩個解密出錯,情況就和 CBC 一樣。
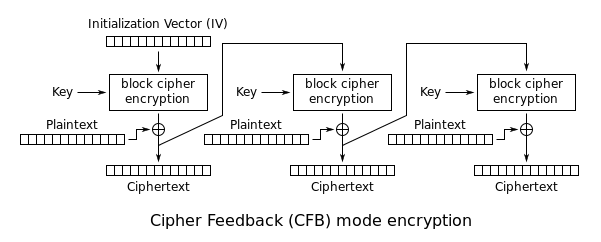
| Encryption: | Decryption: |
| C0 = P0⊕Enc(K, IV) | P0 = C0⊕Enc(K, IV) |
| C1 = P1⊕Enc(K, C0) | P1 = C1⊕Enc(K, C0) |
| . | . |
| . | . |
| . | . |
| Cn = Pn⊕Enc(K, Cn-1) | Pn = Cn⊕Enc(K, Cn-1) |
Symmetric Encryption 對稱式加密
到現在為止,以上所說的加密方法全部是 Symmetric Encryption,原因很簡單,因為加密與解都使用相同的 Key。Symmetric Encryption 在理解上相對簡單,而作速度一般比 Asymmetric 快,因而被廣泛使用。不過 Symmetric Encryption 一直所面對的問題就是 Key 的交換,由於只要得到 Key 就能解密,在傳送 Key 給對方時必需非常僅慎,避免 Key 外洩。
Asymmetric Encryption 非對稱式加密
Asymmetric Encryption 非對稱式加密可謂密碼學上的一大突破!Asymmetric Encryption 中有兩條 Key,分別是 Public Key 與 Private Key。Public Key 是公開的,而 Private Key 只由自己保管。透過 Public Key 加密的密訊可以用 Private Key 解密,相反,使用 Private Key 加密的密訊可以用 Public Key 解密。所以,如果有人想把密訊傳給我,他只要把訊息用我的 Public Key 加密,然後傳給我,我就可以用我的 Private Key 解密。因為只有我自己的 Private Key 可以解密,而我的 Private Key 是不會公開的,這樣就解決了 Symmetric Encryption 需要傳送 Key 的問題。
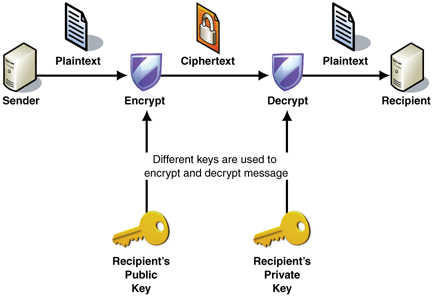
Rivest, Shamir, and Adleman (RSA)
現在介紹第一款 Asymmetric Enccryption 的演算法,稱為 RSA 演算法。計算流程如下:
先選兩個極大的質數 p 與 q,一般長度為 512 bits。為了簡單示範,在本例子中我們用 p=3, q=11。
計算 n = (p)(q) = (3)(11) = 33
計算 Φ (n) = (p – 1)(q – 1) = (2)(10) = 20
假設 Public Key = (e,n) ,Public Key 是公開的,可任意設定 e 值,例如設定成 7,那麽 Public Key 就是 (7,33)。
假設 Private Key = (d,n),計算一個 d 值使 (d)(e) mod Φ (n) = 1
(d)(7) mod 20 = 1
d = 3
所以 Private Key 就是 (3,33)。
假設要加密的訊息是 m = 2,用 Public Key 進行加密,加密公式為密訊 c = m^e mod n
c = 2^7 mod 33 = 29
密訊 c = 29,現在嘗試用 Private Key 解密,解密公式是 m = c^d mod n
m = 29^3 mod 33 = 2
ElGamal Encryption Scheme
第二種演算法為 ElGamal Encryption Scheme。計算流程如下:
先選極大質數 p,為了簡單示範,在本例子中我們用 p=23,
另選常數 g,令 g mod p ≠ 1, g^2 mod p ≠1…… g^(p-2) ≠ 1, 本例子選 g = 11,
選常數 r = 3
設 Private Key x = 6
計算 Public Key y = g^x mod p = 11^6 mod 23 = 9
Public Key y = 9
現為訊息 M = 10 用 Public Key 進行加密:
A = g^r mod p = 11^3 mod 23 = 20
B = (M)(y^r) mod p = (10)(9^3) mod 23 = 22
所以加密訊息 C = (20,22)。
用 Private Key 解密 C = (20,22)
K = A^x mod p = 20^6 mod 23 = 16
M = BK^(-1) mod 23, K^(-1) 的意思是 K 的 Inverse,
K 的 inverse 意思是世上存在一個 K^(-1) 使 KK^(-1) mod 23 = 1
由於 K=16,16K^(-1) mod 23 =1 ,得知 K^(-1) = 13
M = (22)(13) mod 23
M = 10
相關主題
Jan Ho 2014-11-11
Posted In: 其他技術 Others
發佈留言